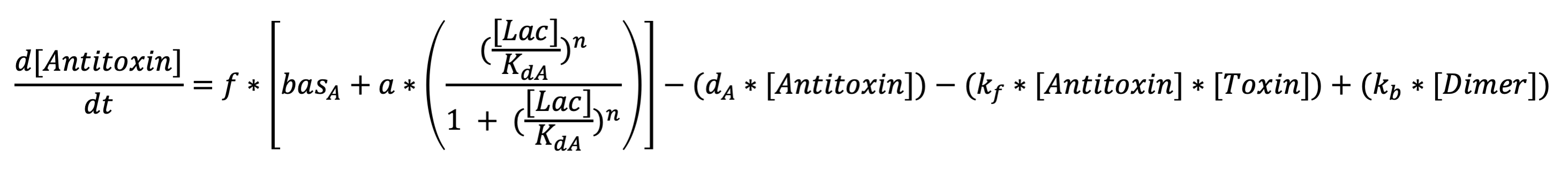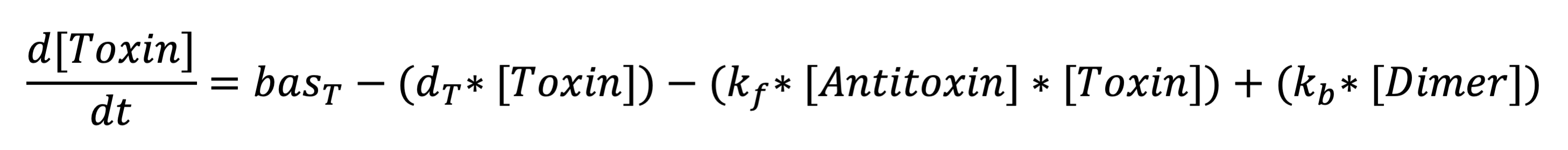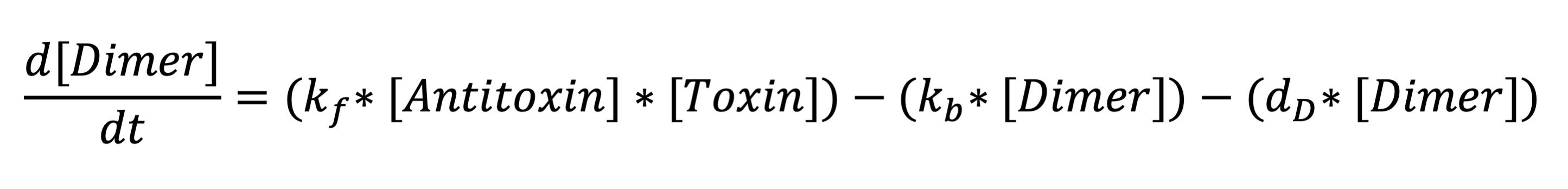Part:BBa_K3419005

Holin/Anti-Holin Kill Switch with Degradation Tag and Lactate Inducible Promoter

Mechanism

Note: All work on this part was done virtually through literature research due to COVID-19 restrictions.

Our kill switch consists of a holin-antiholin toxin-antitoxin system. The holin protein creates holes in the bacterial cell membrane, which allows endolysin protein to pass through and degrade the cell wall, killing the cell. The antiholin protein binds to the holin protein, inactivating it. When both proteins are expressed, whether the cell dies depends on the relative concentrations of both the holin and antiholin components. [1].

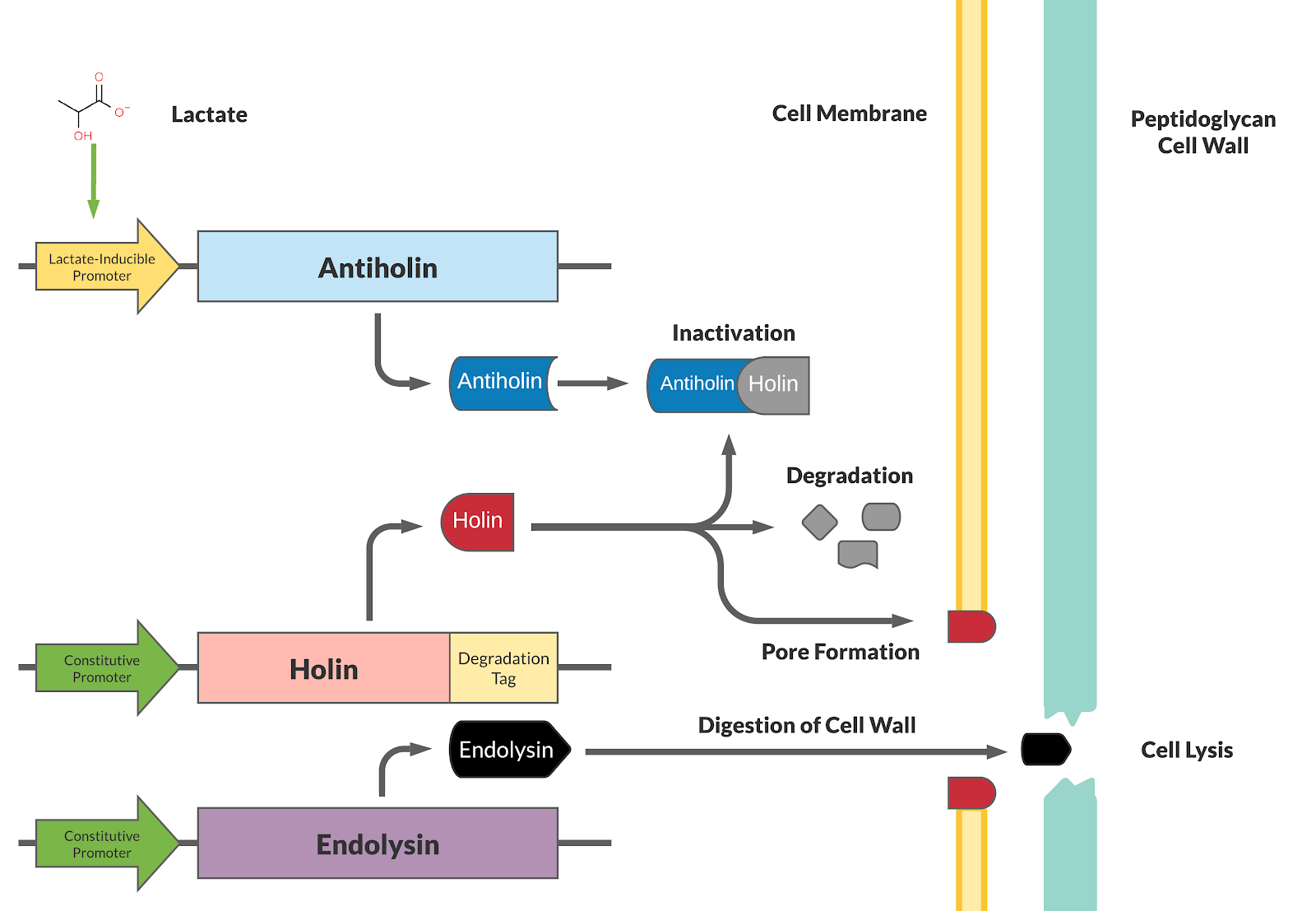
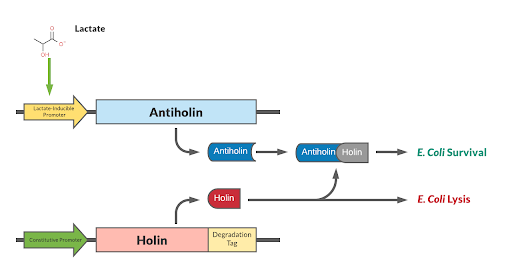
Figure 1. The kill switch consists of three different proteins: holin, which creates holes in the cell membrane; endolysin, which then passes through these holes to degrade the peptidoglycan found in the cell wall; antiholin, which binds to holin to create an inactivated dimer, preventing holes from being formed in the first place [2].

This BioBrick has been designed as a modification to a traditional holin/antiholin kill switch so that the expression of antiholin is controlled by a lactate-inducible promoter, as research shows that lactate concentrations are higher in tumor environments (10-30 mM) compared to healthy tissue (1.5-3 mM) [3]. The toxin, holin, is expressed under a constitutive promoter, as in a typical holin/antiholin kill switch. When in the presence of high lactate, enough antitoxin (antiholin) is produced under the lactate inducible promoter to significantly counteract holin. Otherwise, antiholin is not sufficiently produced, and the bacteria soon die. This allows the bacteria to localize and survive in high-lactate environments such as tumor cells, and die in other environments (i.e. healthy human tissue), as shown in Figure 2.

Figure 2. Diagram depicting the mechanism for the overall kill switch to encourage cell survival in cancerous, or high lactate, environments, and induce cell lysis in healthy tissue.

Improvement

A degradation tag is attached to the holin protein, which marks it for disposal and reduces its half-life in the cell. This limits the activity of the holin toxin prevents its buildup over time, allowing the bacterial population to survive indefinitely as long as it is within a high-lactate tumor environment.

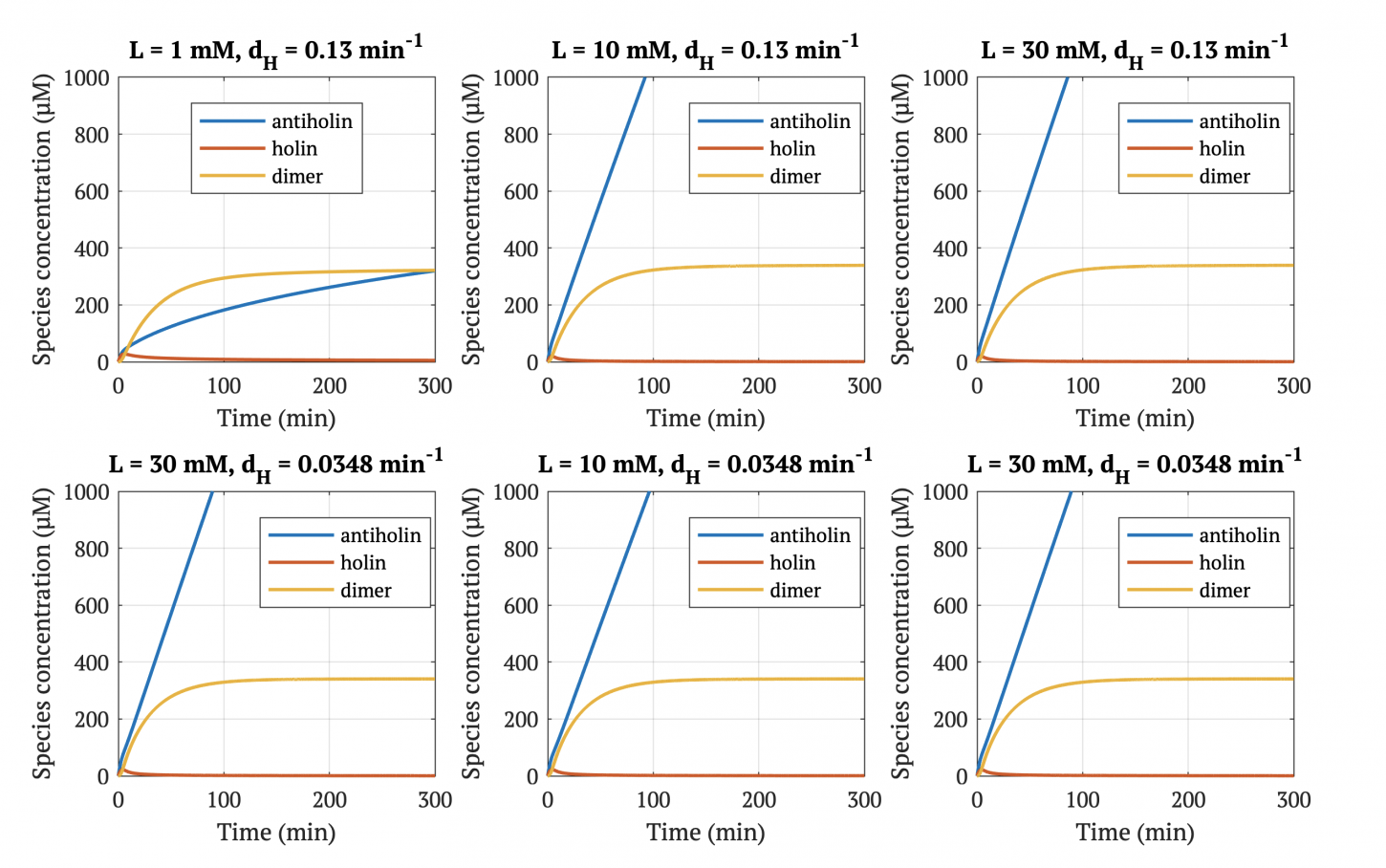
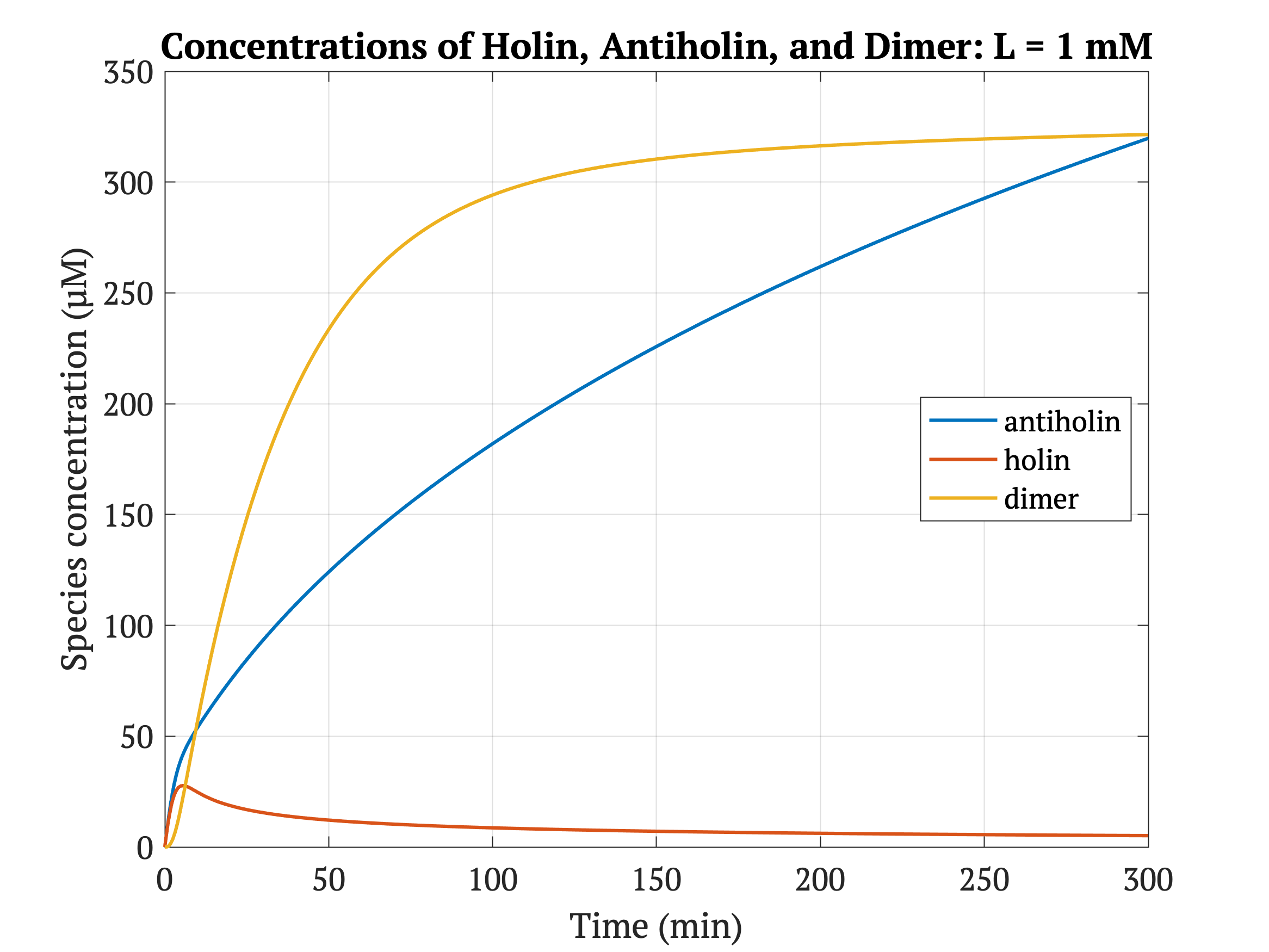
Figure 3. Comparison of the kill switch modeling with a degradation tag (top three plots) show a good distinction between cancerous and non-cancerous tissue. The kill switch without the degradation tag does not make this clear of a distinction (bottom).

With our improved holin part (ie. with degradation tag), there is good distinction between physiologically normal levels of lactate, and cancerous levels of lactate. In other words, with the degradation tag, the bacteria will survive in a tumor environment, and die in healthy tissue.

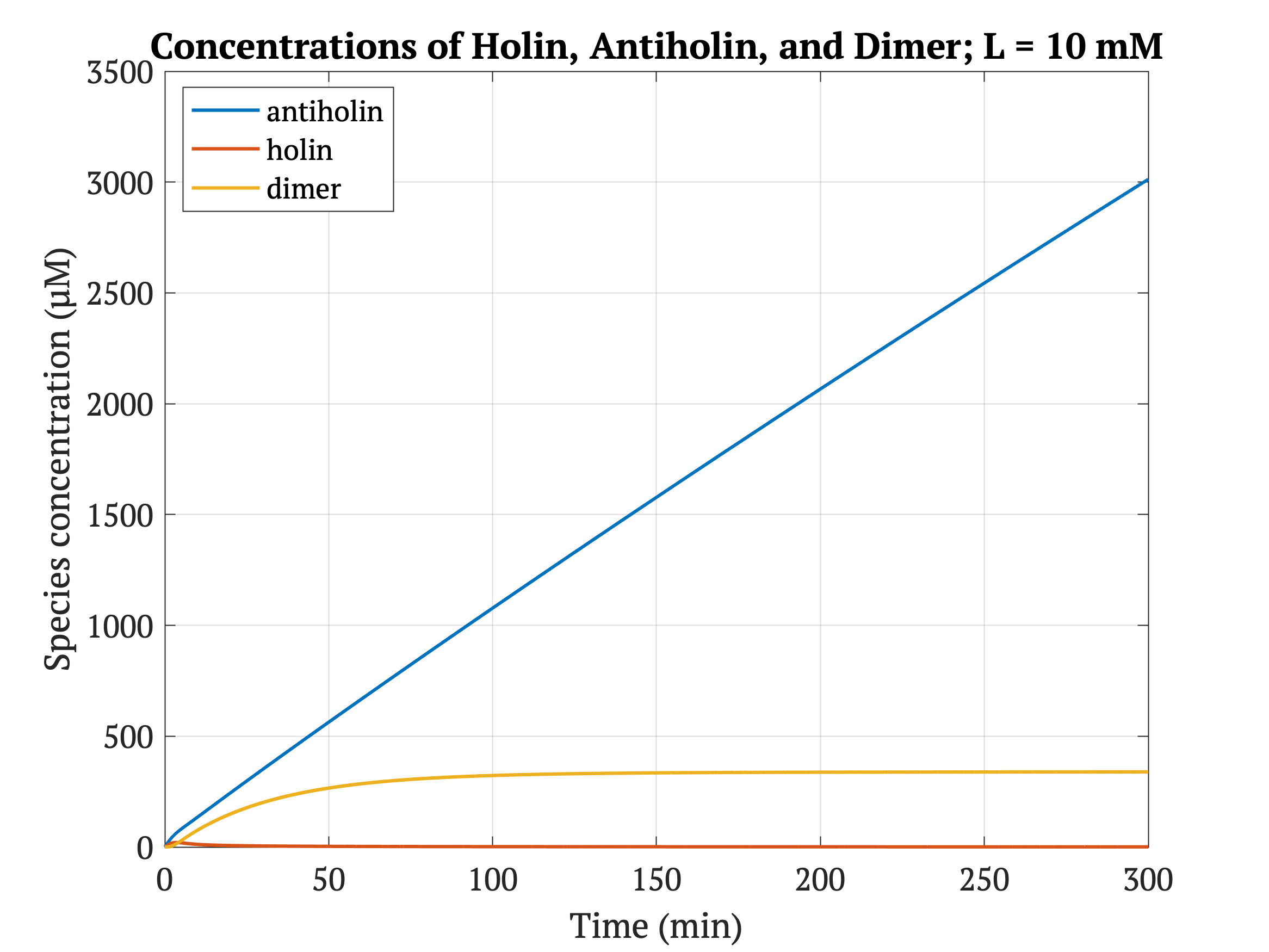
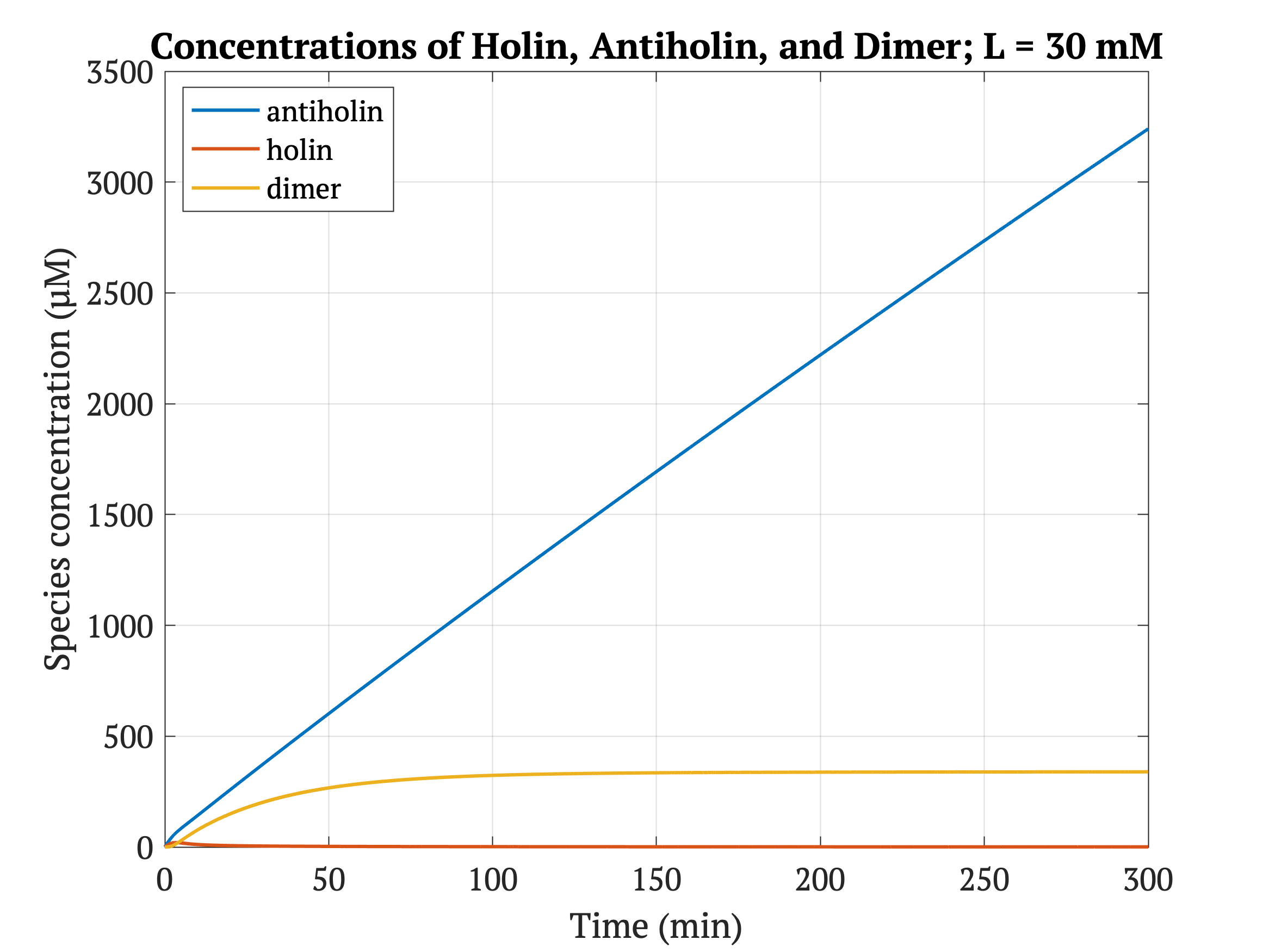
However, without our improvement (ie. without degradation tag), as can be seen in the bottom panel of Figure 3, the holin concentration of all of them is between 0.65 uM and 0.75 uM for concentrations throughout 1 mM to 30 mM, both of which would allow survival. Since this range all allows for bacterial survival, this kill switch would not be specific to cancer tissue without the degradation tag.

Modeling

The following three differential equations were used to model our holin-antiholin kill switch. These equations were solved using Matlab’s built-in ordinary differential equation solver ode45.

The first equation represents the rate at which antiholin is being produced . The terms respectively represent expression from the lactate promoter, removal due to degradation, removal due to the binding to holin (to form the inactivated holin-antiholin dimer), and addition due to disassociation of the holin-antiholin dimer.

Anti-toxin differential equation:

The second equation represents the rate at which holin is being produced. The terms respectively represent the expression from the constitutive promoter, removal due to degradation, removal due to binding to antiholin (to form the inactivated holin-antiholin dimer), and addition due to disassociation of the holin from the holin-antiholin dimer.

Toxin differential equation:

The third equation represents the rate at which the holin-antiholin dimer is formed. The terms respectively represent the reaction rate at which holin and antiholin bind, the rate at which the dimer disassociates, and the rate at which the dimer degrades.

Toxin-antitoxin complex differential equation:

The MATLAB scripts corresponding to the mCardinal modeling can be downloaded here: File:ModelingCodeCornelliGEM2020.zip

Table 1. Parameter Values for Kill Switch Modeling

Variable	Parameter	Value	Source
[Antitoxin]	Concentration of Antitoxin	--	--
[Toxin]	Concentration of Toxin	--	--
[Dimer]	Concentration of toxin-antitoxin dimer	--	--
f	Fluorescent Scaling Factor	= const. expression / (basA + a) = (23.22 uM/min) / (7790 uM/min) = 2.98 *10^-3	[4], [5]
bas_A	Basal expression of lactate promoter	479.3 [uM/min]	[4]
K_dA	Dissociation constant for lactate promoter	1075 [uM]	[4]
n	Exponent	1.326	[4]
a	Induced transcription scaling factor	7311 [uM/min]	[4]
d_A	Rate const, degradation of antitoxin (degradation tag)	0.13 [min^-1]	[6]
d_T	Rate const, degradation of toxin	0.0348 [min^-1]	[1]
[Lac]	Lactate concentration	1 to 30 [mM]	[3]
k_f	Rate const, forward reaction: T + A ↔ TA	1.2 * 10^-4 [uM^-1min^-1]	[1]
k_b	Rate const, reverse reaction: T + A ↔ TA	0.3 * 10^-4 [min^-1]	[4]
bas_T	Basal expression of weak constitutive promoter (assume infinite lactate)	23.22 uM/min for strong promoter J23100, scale by relative strength of J23108 * (1303 / 2547)= 11.87 uM/min= 0.198 [uM/s]	[5], [7]
d_D	Rate const, degradation of toxin-antitoxin dimer	0.0348 [min^-1]	[1]

Figures 4-6 show the concentrations of holin, antiholin, and the inactivated holin-antiholin dimer at different levels of lactate. At a lethal concentration of 1.66 μM, holin kills the bacterial cell [1]. Whether holin reaches this level depends on the relative concentration of antiholin, whose expression is influenced by the lactate level of the surrounding environment.

Figure 4. At 1mM, a very low level of lactate (L) that would be expected outside of the tumor environment, the steady-state concentration of holin is 5.47 μM. This indicates that under these conditions, the bacteria will not infiltrate healthy tissue.

Figure 5. At 10 mM, which is towards the lower end of the tumor lactate level (L) range, the steady-state concentration of holin is 0.59 μM. The bacterial cells will persist and proliferate.

Figure 6. At 30 mM, a high level of lactate (L) that would be expected in the tumor environment, the steady-state concentration of holin is 0.54 μM. The bacterial cell likely survives.

References:

[1] Kill Switch. (2013). Retrieved October 14, 2020, from http://2013.igem.org/KillSwitch

[2] Jie, W. (2014). BBa_K1378032. Retrieved October 13, 2020, from https://parts.igem.org/Part:BBa_K1378032

[3] Cruz-López, K. G., Castro-Muñoz, L. J., Reyes-Hernández, D. O., García-Carrancá, A., & Manzo-Merino, J. (2019). Lactate in the Regulation of Tumor Microenvironment and Therapeutic Approaches. Frontiers in Oncology, 9. doi:10.3389/fonc.2019.01143

[4] Fomitcheva, A. (2015). BBa_K1847009. Retrieved October 14, 2020, from https://parts.igem.org/Part:BBa_K1847009

[5] Yildirim, N., & Mackey, M. C. (2003). Feedback Regulation in the Lactose Operon: A Mathematical Modeling Study and Comparison with Experimental Data. Biophysical Journal, 84(5), 2841-2851. doi:10.1016/s0006-3495(03)70013-7

[6] Guan, R. (2013). BBa_K1051208. Retrieved October 14, 2020, from https://parts.igem.org/Part:BBa_K1051208

[7] Anderson, J. (2006). BBa_J23117. Retrieved October 14, 2020, from https://parts.igem.org/Part:BBa_J23117