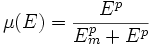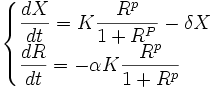Difference between revisions of "Help:Cell-free chassis/Modelling"
Line 2: Line 2:
 
=Cell-Free System modelling=
 
=Cell-Free System modelling=
  
−
==Model assumptions==
+
== Introduction ==
 +
=== Purpose ===
 +
In this section we analyse the data we have obtained on the cell-free chassis using GFP as the reporter. We show that the classic model for the synthesis of a protein by a constitutive promoter is not adapted and introduce a new model where synthesis is curbed by the resources left in the system. Finally we estimate the parameters of this new model from our data and show that it yields a much better fit.
  
−
* Simple constitutive gene expression model
+
=== Prior Knowledge ===
−
* Protein degradation is negligeable (since protease inhibitors are present in the CFS, the rate of proteolytic degradation is minimal)
+
* pTet and pT7 are constitutive promoters that are commonly used ''in vivo'' for ''E. coli''
−
* Resources are an important limiting factor to be considered in our CFS (such as molecules of ATP or protein-charged tRNAs)
+
* [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/CBD1.2 Tests] ''in vitro'' have demonstrated that they also work on the cell-free chassis
 +
* Manufacturer specifications: the solution has been optimised so the degradation of proteins is minimal. We therefore expect our analysis to find very small degradation terms
  
−
==Model description==
+
=== Available Data ===
 +
We need as many data as possible and also data that are as varied as possible (data with similar behaviour will lead to the selection of a model  that is too simple to predict all the behaviours that can be generated by the chassis).
  
−
Although a study of microbial growth rate is undertaken here, this could be altered to feature the system survival/lifetime, as we are dealing with S30 cell extract. The lifetime of the system would be reflected by the rate of change of system energy (''d[nutrient]/dt''), which here is decreasing, as there is no source of replenishment of nutrient.
+
For this section we will use
 +
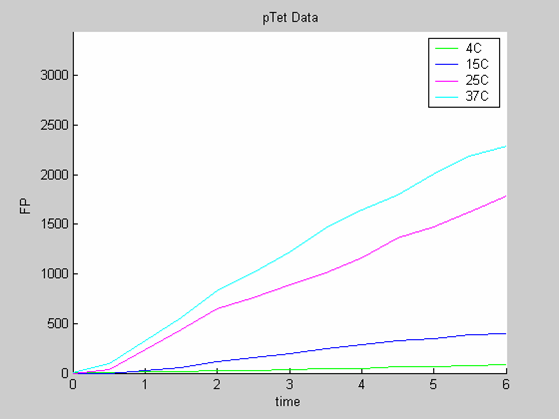
* the [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/CBD2.2 data] collected with pTet at 4,15,25 and 37 degrees that exhibit a linear behaviour
 +
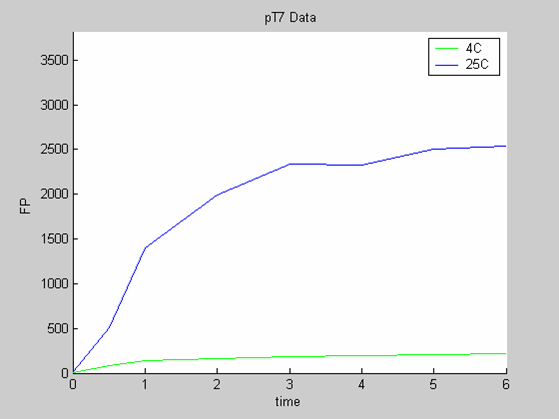
* the pT7 [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/Res1.9 data] at 4 and 25 degrees that exhibit a saturated behaviour.
  
−
A review of literature suggests that multiple models have been developed to describe this feature of the system. The most widely used models are the Monod, Grau, Teisser, Moser and Contois equations.
+
We use the [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/Res1.3 calibration curve of GFP] to convert the fluorescence data into concentrations (in this case the concentrations were express in nanomols/l).
−
<br>
+
−
These equations describe the functional relationship between the microbial growth rate and essential substrate (nutrient) concentration.<br>
+
  
−
It was proposed, and noted from experimental data, that the behaviour of the system can be described as being limited by the energy of the system, and this could be achieved by using the Hill function.<br>
+
{| align="center"
 +
|-
 +
||[[Image:IC07_CFSpTet.png|left|400px]]
 +
||[[Image:IC07_CFSpT7.png|left|400px]]
 +
|}
 +
''Axes: time in hours''<br>
 +
''FP is the concentration of Fluorescent Protein (GFP here) in nanomol/l''
  
−
[[Image:CFS_model_equations.png]]
 
−
'''This equation is partially incorrect - will edit it later'''
 
  
−
{| class="wikitable" border="1" cellspacing="0" cellpadding="2" style="text-align:left; margin: 1em 1em 1em 0; background: #f9f9f9; border: 1px #aaa solid; border-collapse: collapse;"
+
== The Classic Model ==
−
! Parameter                   
+
To analyse our data we use the classic approach that consists of modelling the evolution with time of the concentrations of the product of interest.
−
! Description
+
In this case the model is the simplest we can imagine:
 +
* We have only one protein GFP
 +
* It is constitutively synthesized at a constant synthesis rate K. K depends on the promoter that is used and ourdata show that it is also temperature-dependent
 +
* The protein is then degraded. This degradation term δ depends on the protein and on the chassis. We can assume the impact of temperature to be negligible.
 +
 
 +
The differential equation governing the evolution of X , the concentration of GFP is
 +
[[Image:IC07_CFSeqn1.png|center|100px]]
 +
 
 +
In all cases the initial concentration of GFP was X<sub>0</sub> = 0. The solution of the equation is known explicitly. It is
 +
[[Image:IC07_CFSeqn2.png|center|140px]]
 +
 
 +
{| align="center"
 
|-
 
|-
−
|P || protein concentration
+
||[[Image:IC07_CFSdeg1.png|left|400px]]
 +
||[[Image:IC07_CFSk1.png|left|400px]]
 +
|}
 +
 
 +
 
 +
=== Principle of our Data Analysis ===
 +
 
 +
Instead of analysing each experiment in isolation (for instance pTet at 25 degrees), we used several experiments in coordination.  The idea was to force our data analysis routine  to return only one degradation term for the whole series  of experiment (since the degradation term is chassis-dependent) and one synthesis rate per experiment (the rate K is promoter and temperature dependent, that is in our case experiment-dependent).
 +
 
 +
The algorithm we developed for our data analysis used the scaling properties of the solutions of the differential equations.
 +
We let the time scale of the system (which is the chassis-dependent degradation term δ) run over a range of possible values and then we adjusted for each experiment the amplitude scale (the synthesis rate K) so the interpolation error was minimal for the experiment. The time scale (and the K’s) corresponding to the smallest overall error  were then returned.
 +
 
 +
More details on the algorithm can be found in this complementary documentation (Wiki link to pdf).
 +
 
 +
==== Analysis 1 ====
 +
We first analysed both promoter datasets (the pTet dataset and the pT7)  independently. As can be seen below the model provides a good fit for each dataset.
 +
 
 +
{| align="center"
 
|-
 
|-
−
|E || limiting nutrient/substrate ("energy in system")
+
||[[Image:IC07_CFSpTet1.png|left|400px]]
 +
||[[Image:IC07_CFSpT71.png|left|400px]]
 +
|}
 +
 
 +
The degradation term of the chassis was estimated to be 0.004/hour with the pTet data, which is consistent with statements of the manufacturer of the cell-free extract.  However the pT7 data yield a very high degradation term (0.7/hour).  The difference is high enough to suggest that the cause of such a variation is not rooted in the variability between two batches of cell extract. 
 +
 
 +
==== Analysis 2 ====
 +
When we analyse both datasets together the classic model yields a poor fit to our data as it fails to reconcile the linear behaviour of the pTet data with that of pT7 at 25 degrees (see images below).  The estimated degradation is also high (degradation term = 0.24167)
 +
 
 +
{| align="center"
 
|-
 
|-
−
|&mu; || instantaneous (observed) synthesis rate coefficient
+
||[[Image:IC07_CFSpTet2.png|left|400px]]
 +
||[[Image:IC07_CFSpT72.png|left|400px]]
 +
|}
 +
''Axes: time in hours''<br>
 +
''FP is the concentration of Fluorescent Protein (GFP here) in nanomol/l''
 +
 
 +
''Red crosses= experimental data''<br>
 +
''Full lines: Interpolation''
 +
 
 +
==== Conclusion ====
 +
The results of the data analysis with the classic model strongly '''suggest that the classic model is ill adapted to the description of protein synthesis in our cell free chassis. '''
 +
 
 +
 
 +
== A Resource Dependent Model ==
 +
The classic model cannot reconcile for the same degradation term a linear behaviour and a saturated behaviour. Several publications on systems expressing in cell-free extracts have shown that the lifespan of such systems was shorter than their counterparts in vivo and also that synthesis of proteins declined with time as the system ran out of resources.
 +
 
 +
Such behaviour matches what we can observe for pT7 at 25 degrees. The concentration of GFP climbs steeply but this fast synthesis of GFP exhausts fast the resources of the system. Consequently synthesis grinds to a halt. Since the degradation term is very small in cell free extracts the concentration of GFP remains stable (instead of dropping).
 +
 
 +
We expand the classic model by introducing a function μ that quantifies the limiting effect of the resources available E on the synthesis of GFP.
 +
 
 +
[[Image:IC07_CFSeqn3.png|center|120px]]
 +
 
 +
The more GFP is synthesized the faster the resources drop. We modelled this drop with a linear relation between the resources consumed and the amount of GFP synthesized. We call the ratio a the cost.
 +
Hence
 +
[[Image:IC07_CFSeqn4.png|center|160px]]
 +
 
 +
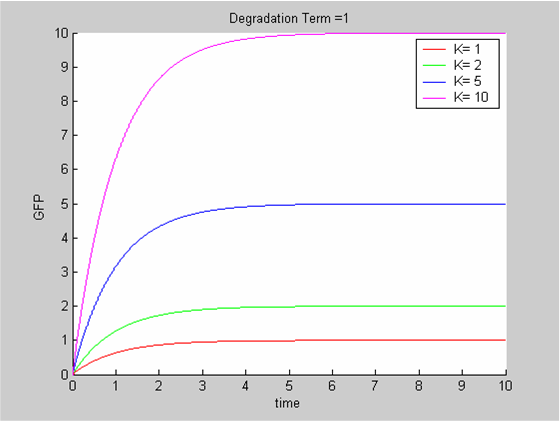
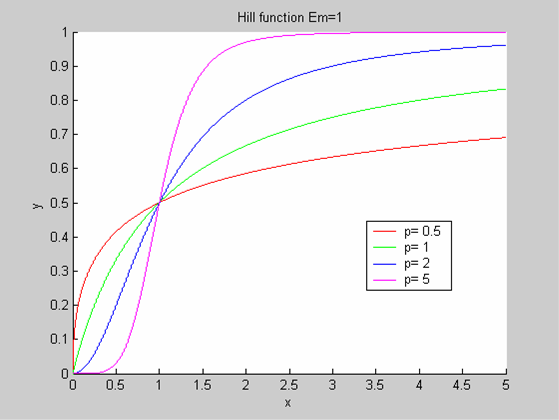
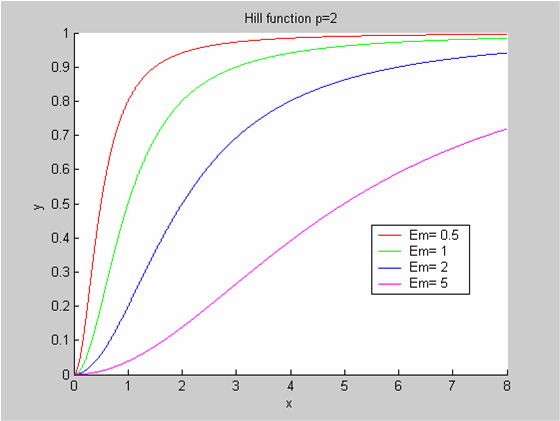
We chose to model the effect μ of the resources available on the synthesis of GFP with a Hill-Function of parameters Em and p. Em is the switching point of the function. The exponent p>=1 determines how steep the switching point is. 
 +
 
 +
* If the model has enough resources E>>Em then μ is almost 1 and the synthesis of GFP proceeds unhinged.
 +
* Conversely when resources are very low, μ is almost zero and synthesis grinds to a halt.
 +
 
 +
[[Image:IC07_CFSeqn5.png|center|200px]]
 +
 
 +
===== Images of Hill Graphs =====
 +
 
 +
{| align="center"
 
|-
 
|-
−
|&mu;<sub>max</sub> || maximal synthesis rate coefficient
+
||[[Image:IC07_CFSh1.png|left|400px]]
 +
||[[Image:IC07_CFSh2.png|left|400px]]
 +
|}
 +
 
 +
Thanks to the scaling properties of the Hill function, our model can be simplified and the chassis-dependent parameter can be eliminated from our model. Indeed it is not the variable E that determines the value of the Resource term μ but the ratio R=E/Em. 
 +
 
 +
The evolution of R is governed by the differential equation
 +
[[Image:IC07_CFSeqn6.png|center|120px]]
 +
 
 +
where the relative cost α directly relates to the cost a  (α=a/ Em).
 +
 
 +
Our resource-dependent model therefore is:
 +
[[Image:IC07_CFSeqn7.png|center|140px]]
 +
 
 +
Its initial conditions are [[Image:IC07_CFSeqn8.png|100px]] at t = 0
 +
 
 +
In this resource-dependent model,
 +
* K is promoter and temperature dependent.
 +
* α, R0 and δ are chassis dependent.
 +
 
 +
== Simulations and Results ==
 +
See [http://parts.mit.edu/igem07/index.php/Imperial/Cell_by_Date/Introduction Cell by Date].
 +
 
 +
==== Data Analysis ====
 +
We tried to estimate the characteristics of the chassis according to our new model. In order to save some computation-time we made the assumption that the degradation terms were negligible (the pTet data and the manufacturer’s claims back this up).
 +
 
 +
The nice properties of the solution of the ODE system with no degradation terms allowed us to restrain the subspace of parameters that needed browsing and to develop an algorithm based on shape matching.
 +
More details on the algorithm we used to analyse the data and estimate the parameters of the model can be found in this complementary documentation (Wiki link to pdf).
 +
 
 +
Results below show the best match that we could obtain for a Hill function of exponent1.
 +
 
 +
'''Please note''' that this time the concentrations are in micromol/l. This change of scale was imposed on us by the ODE45 solver of Matlab that became unstable for the range of values we had to consider (very low α)
 +
 
 +
{| align="center"
 
|-
 
|-
−
|K<sub>s</sub> || half-saturation coefficient
+
||[[Image:IC07_CFSpT73.png|left|400px]]
−
|-
+
||[[Image:IC07_CFSpTet3.png|left|400px]]
−
|&alpha;<sub>1</sub> || energy molecules consumed per synthesis
+
−
|-
+
−
|k<sub>1</sub> || rate of synthesis (promoter concentration and strength)
+
−
|-
+
−
|n || positive co-operativity coefficient
+
 
|}
 
|}
  
−
* mathematical description of the system + parameter info.
+
'''Initial Energy:8'''
−
* see [http://openwetware.org/wiki/User:Jaroslaw_Karcz/Sandbox]
+
'''Cost:3.3333'''
−
* link to SBML file
+
 
 +
'''pT7:'''
 +
K (4 degrees)  = 0.053333
 +
K (25 degrees) = 1.3867
 +
 
 +
'''pTet:'''
 +
K(4 degrees)  = 0.013333
 +
K (15 degrees) = 0.08
 +
K(25 degrees) = 0.34667
 +
K(37 degrees) = 0.49333
 +
 
 +
 
 +
== Available Resources ==
 +
During this summer we have developed many routines with Matlab  which we are happy to share with the rest of Synthetic Biology Community. They can be found in the [http://parts.mit.edu/igem07/index.php/Imperial/Dry_Lab/Software Software Suite] of the [http://parts.mit.edu/igem07/index.php/Imperial/Dry_Lab Dry Lab].
 +
 
 +
The applications that are most relevant to the chassis characterisation are
 +
* '''Constitutive Promoter Analysis'''
 +
Tag a constitutive promoter with a fluorescent protein, record the flurorescence and voila!. This routine loads the data as an excel sheet , allows you to visualize them and if need be to eliminate some samples you do not like.  Then the synthesis rate and degradation term of the milieu are estimated.  The routine was developed so the user may supervise all the operations.
 +
 
 +
* '''Chassis Characterisation with the Classic Promoter Model'''
 +
The routine allows you to load the results of several experiments at the same time. These data are then analysed as described in section 3. Once the best fit is identified, the results are returned and the corresponding graphs are plotted.
  
−
==Simulations: typical beahviours==
+
* '''Chassis Characterisation with the Resource dependent  Model'''
 +
The routine allows you to load the results of several experiments at the same time. These data are then analysed as described in Simulations & Results. Once the best fit is identified, the results are returned and the corresponding graphs are plotted.
  
−
* weak promoter with no degradation (linear production of the output protein) ---> like the pTet data we have
+
Warning: we reduced the subspace of parameters to browse in a way that may not fit your data. The method for doing so is explained in this pdf . We strongly recommend you use a similar method for your data unless you are willing to let your computer run for a very long time (and trust the ODE solver in Matlab…)
−
* strong promoter with no degradation (resources are limiting the rate of synthesis as well as the amount of protein to be produced) ---> like the pT7 data we have
+

Revision as of 05:41, 26 October 2007

Cell-Free System modelling

Introduction

Purpose

In this section we analyse the data we have obtained on the cell-free chassis using GFP as the reporter. We show that the classic model for the synthesis of a protein by a constitutive promoter is not adapted and introduce a new model where synthesis is curbed by the resources left in the system. Finally we estimate the parameters of this new model from our data and show that it yields a much better fit.

Prior Knowledge

  • pTet and pT7 are constitutive promoters that are commonly used in vivo for E. coli
  • [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/CBD1.2 Tests] in vitro have demonstrated that they also work on the cell-free chassis
  • Manufacturer specifications: the solution has been optimised so the degradation of proteins is minimal. We therefore expect our analysis to find very small degradation terms

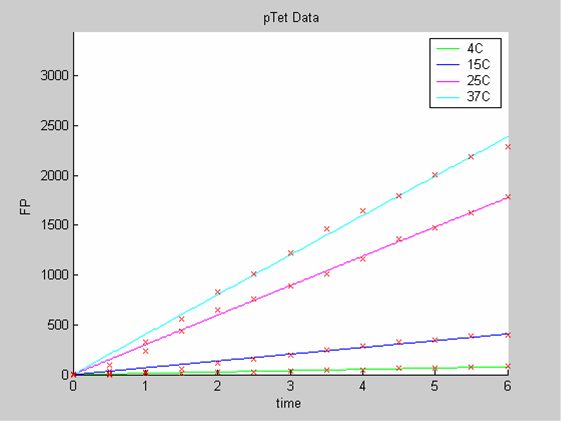
Available Data

We need as many data as possible and also data that are as varied as possible (data with similar behaviour will lead to the selection of a model that is too simple to predict all the behaviours that can be generated by the chassis).

For this section we will use

  • the [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/CBD2.2 data] collected with pTet at 4,15,25 and 37 degrees that exhibit a linear behaviour
  • the pT7 [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/Res1.9 data] at 4 and 25 degrees that exhibit a saturated behaviour.

We use the [http://parts.mit.edu/igem07/index.php/Imperial/Wet_Lab/Results/Res1.3 calibration curve of GFP] to convert the fluorescence data into concentrations (in this case the concentrations were express in nanomols/l).

IC07 CFSpTet.png
IC07 CFSpT7.png

Axes: time in hours
FP is the concentration of Fluorescent Protein (GFP here) in nanomol/l


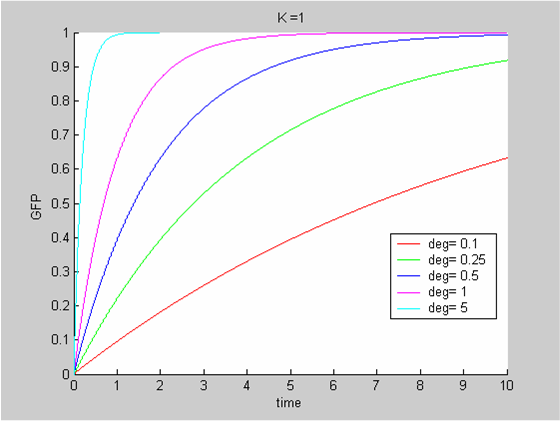
The Classic Model

To analyse our data we use the classic approach that consists of modelling the evolution with time of the concentrations of the product of interest. In this case the model is the simplest we can imagine:

  • We have only one protein GFP
  • It is constitutively synthesized at a constant synthesis rate K. K depends on the promoter that is used and ourdata show that it is also temperature-dependent
  • The protein is then degraded. This degradation term δ depends on the protein and on the chassis. We can assume the impact of temperature to be negligible.

The differential equation governing the evolution of X , the concentration of GFP is

IC07 CFSeqn1.png

In all cases the initial concentration of GFP was X0 = 0. The solution of the equation is known explicitly. It is

IC07 CFSeqn2.png
IC07 CFSdeg1.png
IC07 CFSk1.png


Principle of our Data Analysis

Instead of analysing each experiment in isolation (for instance pTet at 25 degrees), we used several experiments in coordination. The idea was to force our data analysis routine to return only one degradation term for the whole series of experiment (since the degradation term is chassis-dependent) and one synthesis rate per experiment (the rate K is promoter and temperature dependent, that is in our case experiment-dependent).

The algorithm we developed for our data analysis used the scaling properties of the solutions of the differential equations. We let the time scale of the system (which is the chassis-dependent degradation term δ) run over a range of possible values and then we adjusted for each experiment the amplitude scale (the synthesis rate K) so the interpolation error was minimal for the experiment. The time scale (and the K’s) corresponding to the smallest overall error were then returned.

More details on the algorithm can be found in this complementary documentation (Wiki link to pdf).

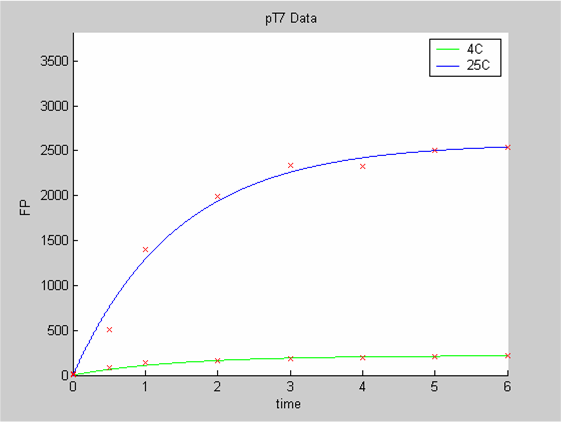
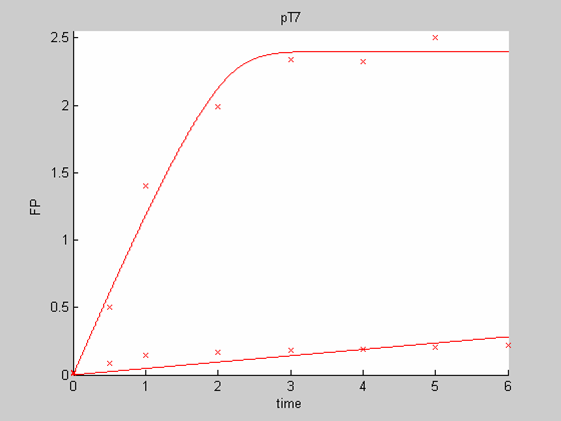
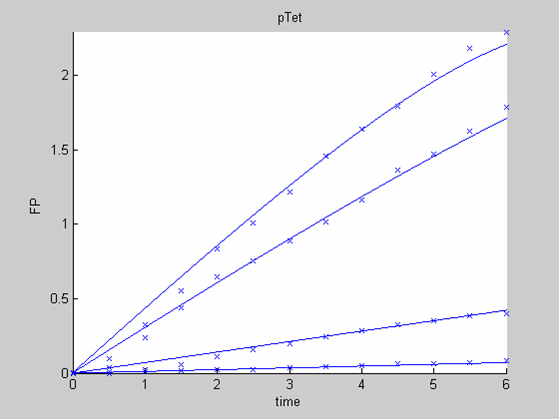
Analysis 1

We first analysed both promoter datasets (the pTet dataset and the pT7) independently. As can be seen below the model provides a good fit for each dataset.

IC07 CFSpTet1.png
IC07 CFSpT71.png

The degradation term of the chassis was estimated to be 0.004/hour with the pTet data, which is consistent with statements of the manufacturer of the cell-free extract. However the pT7 data yield a very high degradation term (0.7/hour). The difference is high enough to suggest that the cause of such a variation is not rooted in the variability between two batches of cell extract.

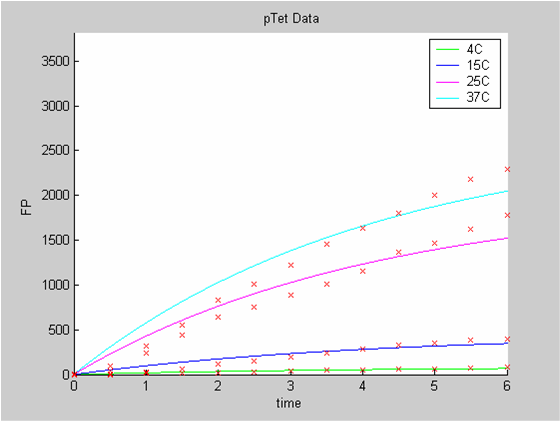
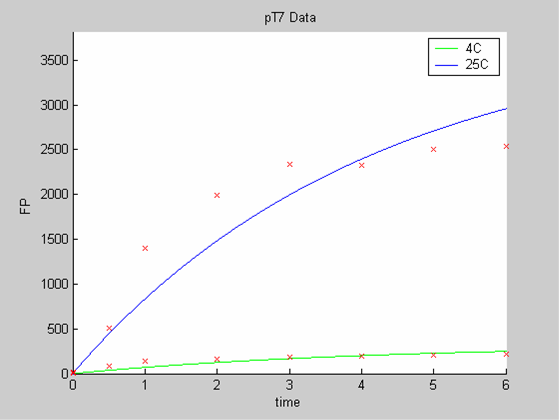
Analysis 2

When we analyse both datasets together the classic model yields a poor fit to our data as it fails to reconcile the linear behaviour of the pTet data with that of pT7 at 25 degrees (see images below). The estimated degradation is also high (degradation term = 0.24167)

IC07 CFSpTet2.png
IC07 CFSpT72.png

Axes: time in hours
FP is the concentration of Fluorescent Protein (GFP here) in nanomol/l

Red crosses= experimental data
Full lines: Interpolation

Conclusion

The results of the data analysis with the classic model strongly suggest that the classic model is ill adapted to the description of protein synthesis in our cell free chassis.


A Resource Dependent Model

The classic model cannot reconcile for the same degradation term a linear behaviour and a saturated behaviour. Several publications on systems expressing in cell-free extracts have shown that the lifespan of such systems was shorter than their counterparts in vivo and also that synthesis of proteins declined with time as the system ran out of resources.

Such behaviour matches what we can observe for pT7 at 25 degrees. The concentration of GFP climbs steeply but this fast synthesis of GFP exhausts fast the resources of the system. Consequently synthesis grinds to a halt. Since the degradation term is very small in cell free extracts the concentration of GFP remains stable (instead of dropping).

We expand the classic model by introducing a function μ that quantifies the limiting effect of the resources available E on the synthesis of GFP.

IC07 CFSeqn3.png

The more GFP is synthesized the faster the resources drop. We modelled this drop with a linear relation between the resources consumed and the amount of GFP synthesized. We call the ratio a the cost. Hence

IC07 CFSeqn4.png

We chose to model the effect μ of the resources available on the synthesis of GFP with a Hill-Function of parameters Em and p. Em is the switching point of the function. The exponent p>=1 determines how steep the switching point is.

  • If the model has enough resources E>>Em then μ is almost 1 and the synthesis of GFP proceeds unhinged.
  • Conversely when resources are very low, μ is almost zero and synthesis grinds to a halt.
IC07 CFSeqn5.png
Images of Hill Graphs
IC07 CFSh1.png
IC07 CFSh2.png

Thanks to the scaling properties of the Hill function, our model can be simplified and the chassis-dependent parameter can be eliminated from our model. Indeed it is not the variable E that determines the value of the Resource term μ but the ratio R=E/Em.

The evolution of R is governed by the differential equation

IC07 CFSeqn6.png

where the relative cost α directly relates to the cost a (α=a/ Em).

Our resource-dependent model therefore is:

IC07 CFSeqn7.png

Its initial conditions are IC07 CFSeqn8.png at t = 0

In this resource-dependent model,

  • K is promoter and temperature dependent.
  • α, R0 and δ are chassis dependent.

Simulations and Results

See [http://parts.mit.edu/igem07/index.php/Imperial/Cell_by_Date/Introduction Cell by Date].

Data Analysis

We tried to estimate the characteristics of the chassis according to our new model. In order to save some computation-time we made the assumption that the degradation terms were negligible (the pTet data and the manufacturer’s claims back this up).

The nice properties of the solution of the ODE system with no degradation terms allowed us to restrain the subspace of parameters that needed browsing and to develop an algorithm based on shape matching. More details on the algorithm we used to analyse the data and estimate the parameters of the model can be found in this complementary documentation (Wiki link to pdf).

Results below show the best match that we could obtain for a Hill function of exponent1.

Please note that this time the concentrations are in micromol/l. This change of scale was imposed on us by the ODE45 solver of Matlab that became unstable for the range of values we had to consider (very low α)

IC07 CFSpT73.png
IC07 CFSpTet3.png

Initial Energy:8 Cost:3.3333

pT7: K (4 degrees) = 0.053333 K (25 degrees) = 1.3867

pTet: K(4 degrees) = 0.013333 K (15 degrees) = 0.08 K(25 degrees) = 0.34667 K(37 degrees) = 0.49333


Available Resources

During this summer we have developed many routines with Matlab which we are happy to share with the rest of Synthetic Biology Community. They can be found in the [http://parts.mit.edu/igem07/index.php/Imperial/Dry_Lab/Software Software Suite] of the [http://parts.mit.edu/igem07/index.php/Imperial/Dry_Lab Dry Lab].

The applications that are most relevant to the chassis characterisation are

  • Constitutive Promoter Analysis

Tag a constitutive promoter with a fluorescent protein, record the flurorescence and voila!. This routine loads the data as an excel sheet , allows you to visualize them and if need be to eliminate some samples you do not like. Then the synthesis rate and degradation term of the milieu are estimated. The routine was developed so the user may supervise all the operations.

  • Chassis Characterisation with the Classic Promoter Model

The routine allows you to load the results of several experiments at the same time. These data are then analysed as described in section 3. Once the best fit is identified, the results are returned and the corresponding graphs are plotted.

  • Chassis Characterisation with the Resource dependent Model

The routine allows you to load the results of several experiments at the same time. These data are then analysed as described in Simulations & Results. Once the best fit is identified, the results are returned and the corresponding graphs are plotted.

Warning: we reduced the subspace of parameters to browse in a way that may not fit your data. The method for doing so is explained in this pdf . We strongly recommend you use a similar method for your data unless you are willing to let your computer run for a very long time (and trust the ODE solver in Matlab…)