Difference between revisions of "Part:BBa K2601008"
LebronJames (Talk | contribs) |
LebronJames (Talk | contribs) |
||
| Line 24: | Line 24: | ||
[[file:T--Peking--FKBP-Frb-image2.png|500px|thumb|center|<b>Figure 3.</b>]] | [[file:T--Peking--FKBP-Frb-image2.png|500px|thumb|center|<b>Figure 3.</b>]] | ||
| + | |||
| + | To quantify the system’s evolution, we choose the Flory-Huggins model to characterize the thermodynamics and the stochastic Cahn-Hilliard equation to describe the kinetics of phase separation process. For the first equation, F is the free energy of the whole system. φ is volume fraction of each component. The first term represents the entropy of mixing, which tend to keep the molecules well-mixed. The second term represents the interaction energy, which is governed by the interaction parameter, chi. The third term (gradient free energy) is related to surface tension. For the second equation, φ simply relaxes toward equilibrium at a rate proportional to the local chemical potential, which is delta F divides by delta φ. | ||
| + | To begin with, we referred to a simplified system comprising only two components. In the absence of interaction energy, the mixing energy generally drives the mixing of initially unmixed components. But when the interaction energies that favor the like neighbors and disfavor the unlike neighbors exist. There are two low free energy states. Then the mixture with a composition φ decompose into two regions, each of volume fraction φs and φD. The free energy of the demixing state is indicated by the dotted line, which is lower than free energy of the homogenous mixture. | ||
| + | The free energy is shown as the light blue curve. | ||
| + | the free energy is shown as the dark blue curve. | ||
| + | turn to the thermodynamic model of our system. Phase separation is easy to take place in the green area, where the system is unstable, while it can also happen in the blue area, where the system is metastable. Whether chi one three is equal to chi two three decides whether the diagram is symmetric. This is a useful instruction for our experiments. To some extends it can save us from some unnecessary trials. | ||
| + | Here are the kinetic simulation results. We can see the larger chi is, the sooner the system relaxes into equilibrium state, which means the faster the phase separation appears. | ||
| + | |||
<table border="0" align="center"> <tr> <td>[[file:T--Peking--promoter-strength.png|300px]]</td> <td>[[file:T--Peking--FKBP-Frb-promoter.png|300px]]</td> <td>[[file:T--Peking--thermo-model.png|300px]]</td> </tr><tr><td colspan="3"><b>Figure 4.</b></td></tr> </table> | <table border="0" align="center"> <tr> <td>[[file:T--Peking--promoter-strength.png|300px]]</td> <td>[[file:T--Peking--FKBP-Frb-promoter.png|300px]]</td> <td>[[file:T--Peking--thermo-model.png|300px]]</td> </tr><tr><td colspan="3"><b>Figure 4.</b></td></tr> </table> | ||
Revision as of 16:16, 14 October 2018
FKBP-yEGFP
Introduction
A widespread use of rapamycin, an anti-fungal antibiotic, has been developed to take advantage of the small molecule’s ability to heterodimerize proteins. Rapamycin binds to the FK506 binding protein (FKBP) as well as to a 100-amino acid domain of the mammalian target of rapamycin (mTOR), known as the FKBP-rapamycin binding domain (Frb). Proteins of interest can be expressed as fusions to FKBP or Frb, and then conditionally dimerized by adding rapamycin.
Design
Some membrane-less organelles, such as stress granules and P bodies, have been discovered in recent years. Proteins condense into droplets and assemble these organelles through a process called phase separation. Physically, phase separation is the transformation of a one-phase thermodynamic system to a multi phase system, much like how oil and water demix from each other. According to thermodynamics, molecules will diffuse down the gradient of chemical potential instead of concentration. This is exactly why proteins will self organize into granules, diffusing from regions of low concentration to regions of high concentration. Here is an illustration of phase separation in cells.
 |  |  |
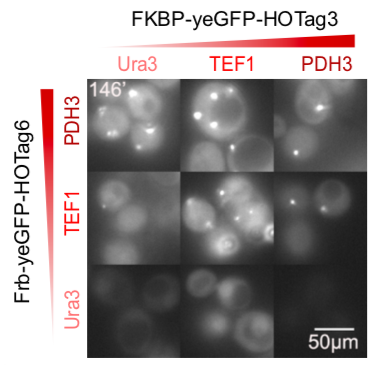
In order to rationally design a synthetic organelle based on protein phase separation, we need a multivalent module and a protein-protein interaction module. The paired FKBP and Frb is one of the bioparts that we chose to introduce protein-protein interaction. FKBP and Frb can dimerize upon adding rapamycin. As for the multivalent module, we turned to de novo-designed homo-oligomeric short peptides. These short peptides are called HO-Tags (homo-oligomeric tags). HOTags contain approximately 30 amino acids. HOTags have high stoichiometry, forming hexamer or tetrameric spontaneously. The hexameric HOTag3, together with the tetrameric HOTag6, can robustly drive protein phase separation upon protein interaction (achieved by FKBP-Frb module). We named our system SPOT(Synthetic Phase separation-based Organelle Platform) because it can form granules (fluorescent spots) in yeast. To verify the feasibility of the system, we fused two fluorescence proteins with the two components of synthetic organelles. Thus, we can observe the self-organization of components and the formation of organelles under fluorescence microscope. Here is a demonstration of our overall design.
Properties
The interaction between FKBP and rapamycin has been well characterized (Kd ≈ 0.2 nM), and early experiments suggest that formation of a ternary complex including FRB is quite favorable (Kd ≈ 2.5 nM). FKBP and FRB do not interact in the absence of rapamycin. Our results confirm that FKBP/Frb module fused with HOTags can drive phase separation in yeast.
To quantify the system’s evolution, we choose the Flory-Huggins model to characterize the thermodynamics and the stochastic Cahn-Hilliard equation to describe the kinetics of phase separation process. For the first equation, F is the free energy of the whole system. φ is volume fraction of each component. The first term represents the entropy of mixing, which tend to keep the molecules well-mixed. The second term represents the interaction energy, which is governed by the interaction parameter, chi. The third term (gradient free energy) is related to surface tension. For the second equation, φ simply relaxes toward equilibrium at a rate proportional to the local chemical potential, which is delta F divides by delta φ.
To begin with, we referred to a simplified system comprising only two components. In the absence of interaction energy, the mixing energy generally drives the mixing of initially unmixed components. But when the interaction energies that favor the like neighbors and disfavor the unlike neighbors exist. There are two low free energy states. Then the mixture with a composition φ decompose into two regions, each of volume fraction φs and φD. The free energy of the demixing state is indicated by the dotted line, which is lower than free energy of the homogenous mixture.
The free energy is shown as the light blue curve.
the free energy is shown as the dark blue curve.
turn to the thermodynamic model of our system. Phase separation is easy to take place in the green area, where the system is unstable, while it can also happen in the blue area, where the system is metastable. Whether chi one three is equal to chi two three decides whether the diagram is symmetric. This is a useful instruction for our experiments. To some extends it can save us from some unnecessary trials. Here are the kinetic simulation results. We can see the larger chi is, the sooner the system relaxes into equilibrium state, which means the faster the phase separation appears.
 |  |  |
| Figure 4. | ||
Sequence and Features
- 10COMPATIBLE WITH RFC[10]
- 12COMPATIBLE WITH RFC[12]
- 21INCOMPATIBLE WITH RFC[21]Illegal BglII site found at 337
Illegal BamHI site found at 358 - 23COMPATIBLE WITH RFC[23]
- 25INCOMPATIBLE WITH RFC[25]Illegal AgeI site found at 79
- 1000INCOMPATIBLE WITH RFC[1000]Illegal BsaI.rc site found at 1004